Et un sudoku offert
Attention, moins il y a de chiffres au début, plus c'est difficile!
posted by LCTM @ 21:54
8 comments
Transatlantique en solitaire
Vous voilà sur mon blog. La raison d'être de ce blog, si elle en a une, est là, là, et enfin LÀ.
NB: Toi qui, comme moi, es gavé par ces gens qui écrivent des pages et des pages, j'ai pensé à toi.
Contente-toi de lire le résumé à la fin de chaque note, tu ne perdras pas grand chose.Va aussi voir le dernier "là".
Monday, April 17, 2006
8 Comments:
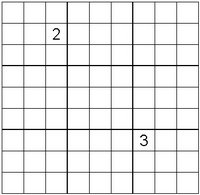
Claim : The solution is not unique.
Proof : Given a solution, any permutation of any two symbols (excluding 2 and 3) gives another solution.
As for the existence, any permutation of most existing completed Sudoku grids trivially proves it.
I'm not sure you're right.
Well.. I am..
Imagine this grid, completed in a sudoku-valid way, with all the symbols from 1 to 9 and stuff.
Now you have to realize that sudoku is essentially symbol invariant - that is, if you replace all the 1s in the grid with 5s, and all the 5s with 1s, the resulting grid is still sudoku-valid. Actually, you could even replace 1s with hearts, 2s with spades, or whatever.
In most (if not all) grids available in newspapers, all the existing symbols (or maybe only eight of them) are represented at the start. Is it sufficient to guarantee unicity? I do not know. But I do claim that it is necessary.
O ure right... but i think its not sufficient.
Let me tell ya this sudoku wasnt serious.
I know, pal, I know
You're so wise, 2...
Hey, I am not sure that is necessary. Imagine you have all numbers initially present on the grid, but one. Your condition is not fullfilled, though there could be a unique solution.
"In most (if not all) grids available in newspapers, all the existing symbols (or maybe only eight of them) are represented at the start. Is it sufficient to guarantee unicity?"
I thought about it indeed. Eight is necessary for sure. But anyway. Life is not a sudoku grid.
Post a Comment
<< Home